Rapport
Introduction
Les illusions d’optique témoignent des limites, mais aussi de l’ingéniosité de notre perception visuelle. Parmi elles, les figures de Kanizsa, pour lesquelles notre perception complète des formes absentes à partir d’indices visuels fragmentaires, illustrent parfaitement la capacité du cerveau humain à générer du sens à partir du vide. Dans un tout autre domaine, celui des intelligences artificielles, les modèles de diffusion ont une capacité similaire: celle de créer du sens à partir de bruit.
Ces nouveaux modèles génératifs, capables de produire des images réalistes à partir d’une simple description textuelle, offrent un champ expérimental nouveau et nous mènent à notre problématique principale : “Est-ce-qu’une IA peut générer ou percevoir une illusion visuelle, sans l’avoir explicitement apprise ?”.
Notre TER s’inscrit dans cette interrogation. Nous avons cherché à explorer la convergence entre le fonctionnement des modèles de diffusion, qui partent d’un bruit pour “compléter” progressivement une image, et les mécanismes cognitifs de complétion perceptive observés chez l’humain.
Pour cela, nous avons mis en place un protocole expérimental associant génération automatique d’images à l’aide du modèle de diffusion Stable Diffusion, et évaluation humaine via une expérience intégrée à un site web. L’objectif est de tester la capacité de l’IA à produire des illusions visuelles de type Kanizsa de manière autonome, et analyser les facteurs qui influencent cette capacité. Cette étude s’inscrit dans une double perspective : mieux comprendre les capacités créatives et d'interprétation des IA génératives, mais aussi chercher de nouvelles pistes sur la modélisation des processus perceptifs humains.
Dans ce mémoire, nous commencerons par présenter le cadre théorique reliant IA, modèles de diffusion et illusions d’optique. Nous exposerons ensuite la problématique qui a guidé notre recherche, le protocole mis en place, ainsi que les outils développés pour générer et tester les images. Enfin, nous analyserons les résultats obtenus et discuterons des perspectives offertes par cette exploration à la frontière entre art visuel, cognition et intelligence artificielle.
I ) PREMIÈRE PARTIE - CADRE THÉORIQUE
1 ) Approche générale des modèles de diffusion
1.1 ) Intelligence Artificielle
Les modèles de diffusion (MD) sont un type d'algorithme qui fait partie de l’immense famille des Intelligences Artificielles (IA). Dans cette grande famille, les MD se situent dans le sous-ensemble des algorithmes de Deep Learning, lui-même inclus dans l’ensemble du Machine Learning. Pour que ce soit plus clair, nous pouvons représenter ces inclusions sous la forme du diagramme de Venn suivant :
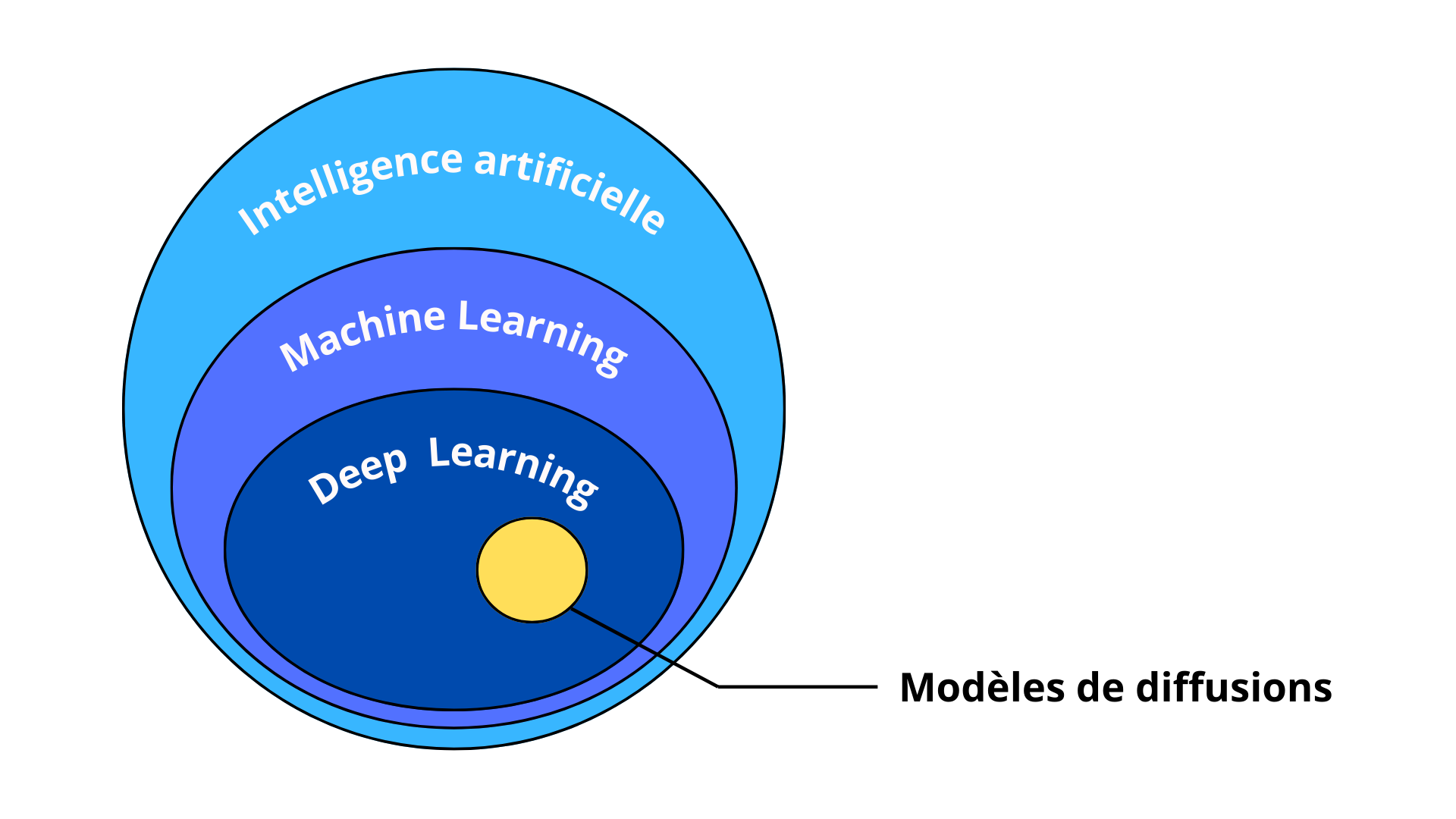
Figure 1. Diagramme de Venn des catégories d’intelligences artificielles
L’IA regroupe toutes les méthodes qui permettent à une machine de réaliser des tâches nécessitant normalement des fonctions cognitives humaines, comme apprendre, raisonner, percevoir ou communiquer. À l’origine, les IA n’étaient constituées que d’arbres de décisions basés sur des règles logiques élémentaires (SI, ET, OU… ), celles-ci sont aujourd’hui appelées GOFAI pour Good Old Fashioned Artificial Intelligence (Boden, 2014 [1]). À l’opposé du paradigme des GOFAI se trouve le machine learning. Cette approche rejoint une autre vision de l’intelligence artificielle appelée connexionnisme.
Contrairement à la GOFAI, le connexionnisme s’inspire du fonctionnement du cerveau humain, et plus particulièrement du cortex. Il modélise l’intelligence comme un ensemble de réseaux de neurones interconnectés, capables d’apprendre en adaptant les forces de connexion entre les neurones. Le machine learning moderne s'inscrit directement dans cette tradition connexionniste. Dans cette continuité, le deep learning se distingue par l’utilisation de réseaux de neurones profonds, c’est-à-dire composés de nombreuses couches successives de neurones, là où pour le machine learning la couche de sortie est directement reliée à la couche d’entrée. Cette profondeur permet au modèle de construire progressivement des représentations hiérarchiques et abstraites des données. C’est précisément dans ce cadre que s’inscrivent les modèles de diffusion.
1.2 ) Cas particuliers des modèles de diffusion
Les modèles de diffusion appliqués à la génération d'images reposent sur un processus itératif de dégradation et de restauration des images. L’objectif est de transformer une image réelle en une version bruitée, puis de reconstruire cette image à partir du bruit, étape par étape, dans le but de générer des images nouvelles et réalistes.
a ) Entraînement du modèle
L'entraînement d'un modèle de diffusion se base sur les processus appelés diffusion directe (forward process) et son inverse, la diffusion inverse (reverse process). L’idée principale consiste à apprendre à un réseau de neurones à reconstruire une image à partir d’une version bruitée de celle-ci (Geng, Park, & Owens, 2025 [2]).
Le processus débute par la prise d’images réelles issues d’une base de données. À chaque itération, un bruit blanc gaussien est ajouté à l’image, de manière progressive, jusqu’à ce que celle-ci devienne pratiquement indistinguable du bruit pur. Cette phase de dégradation correspond à la diffusion directe, qui est un processus connu et déterministe.
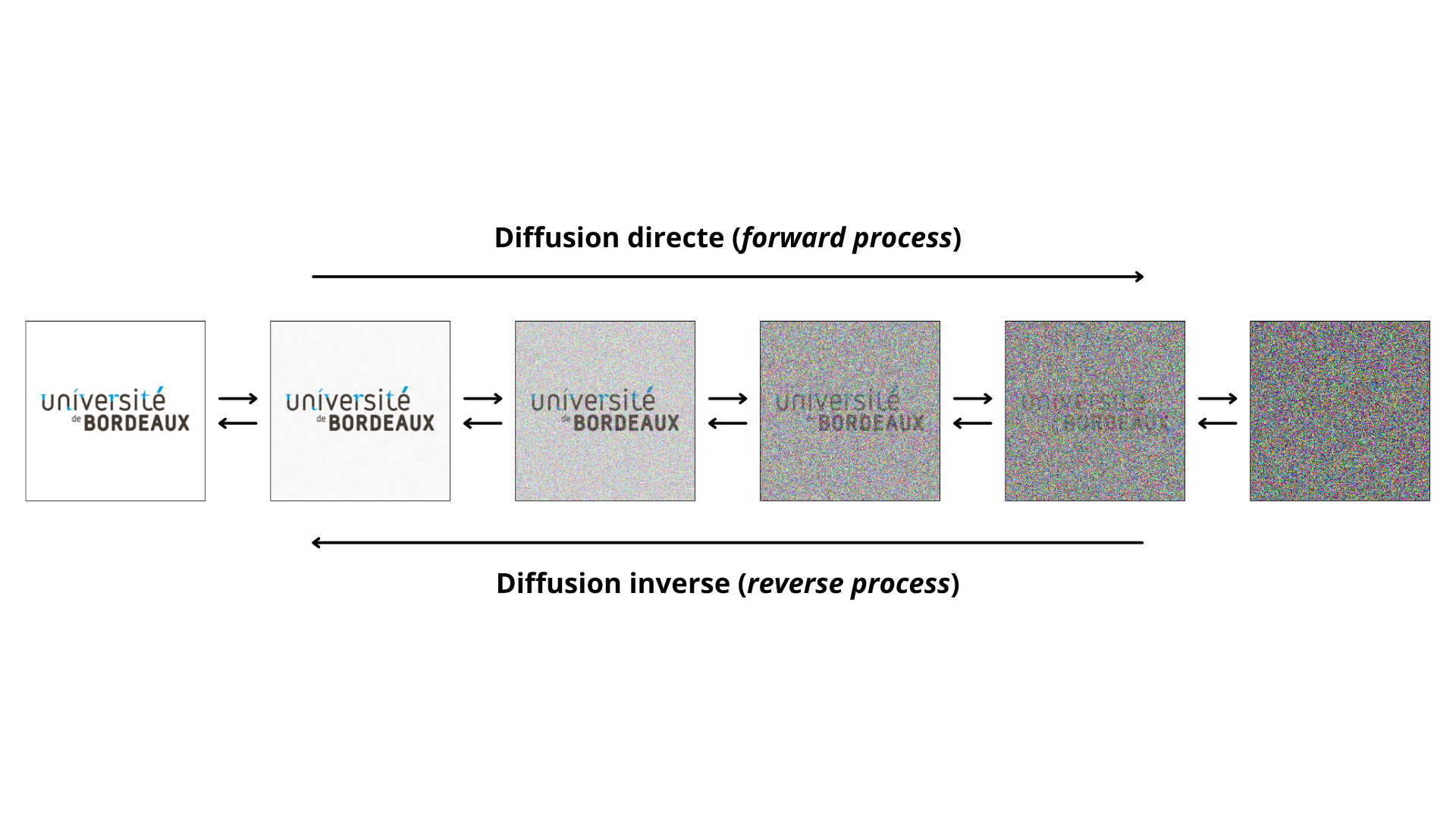
Figure 2. Principe du processus de diffusion dans un modèle de génération d’images
La diffusion inverse est le processus qu’apprend le modèle durant l'entraînement. Il s’agit de la reconstruction progressive de l’image initiale à partir d’une version bruitée. Contrairement à la diffusion directe, ce processus est inconnu a priori et doit être appris par un réseau de neurones autoencoder, généralement un U-Net. Un U-Net est un réseau de neurones basé sur l'architecture dite entièrement convolutionnelle (fully convolutional networks), cette architecture permet en partie de réduire la taille des données à chaque couche sur la première partie du U-Net, puis de reconstruire les données sur la seconde partie. Il s’agit d’un algorithme autoencoder avec la particularité que chacune des couches de l’encoder est directement liées à la couche du décodeur de même taille. Cette particularité permet notamment de garder la localisation des informations dans l’image.
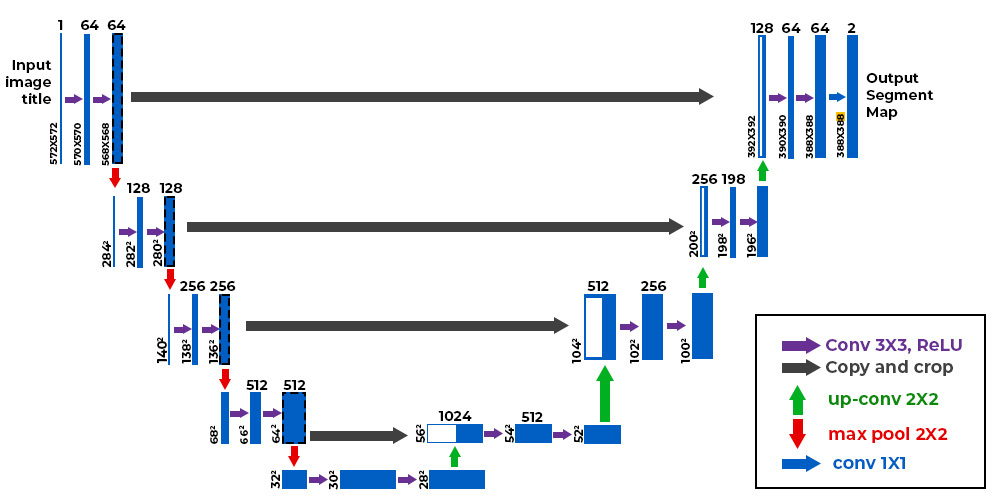
Figure 3. Exemple d’architecture U-Net
À chaque étape, le modèle reçoit une image bruitée et tente de prédire le bruit ajouté. En soustrayant ce bruit estimé, il obtient une version légèrement moins bruitée de l’image. Cette opération est répétée de manière itérative, en affinant progressivement le signal, jusqu’à obtenir une image nette et cohérente. C’est une dénormalisation graduelle, qui transforme du bruit aléatoire en une image réaliste.
b ) Génération des images
Une fois entraîné, le modèle est capable de générer de nouvelles images réalistes à partir d’un simple bruit, sans qu’aucune image d’origine ne soit nécessaire.
Cependant, pour que le modèle ne produise pas une image purement aléatoire, il doit être conditionné par une information d’entrée, comme un prompt textuel. Le modèle reçoit alors, en plus de l’image de bruit pur, une condition (par exemple un texte décrivant ce qu’il doit générer). Cette condition est intégrée dans le réseau de neurones à l’aide d’un module d’encodage du texte dont les représentations sont injectées dans le U-Net à différents niveaux.
Ainsi, à chaque étape du processus de débruitage, le modèle ne cherche pas seulement à réduire le bruit, mais à orienter la reconstruction vers une image qui respecte la condition donnée. Cela permet de générer des images qui ne sont pas seulement réalistes, mais pertinentes et alignées avec le prompt fourni.
Le modèle dispose de différents hyperparamètres qui ont un impact sur le résultat final, c’est-à-dire la génération de l’image. Les principaux (Figure 4) sont :
- Le prompt : c’est la description textuelle de ce qu’on souhaite générer
- Le negative prompt : représente la liste des éléments que l’on ne veut pas voir dans l’image générée
- Les samplings steps : ce paramètre indique le nombre d’itérations de raffinement de l’image. C’est-à-dire le nombre de passages que l’IA fera sur notre image. A chaque passage, l’IA améliorera l’image, donc plus la valeur est élevée, plus l’image sera détaillée mais avec un temps de calcul plus important
- La size : il s’agit de la taille de l’image qui sera générée. Par défaut, ce sera 512 pixels (width) par 512 pixels (height)
- Le batch count : nombre de lots différents à générer
- Le batch size : nombre d’images simultanées par lot
- Le CFG Scale : ce réglage permet d’indiquer à l’IA à quel point elle doit respecter notre demande. Une valeur trop grande limite la créativité tandis qu’une valeur trop petite donne trop de liberté.
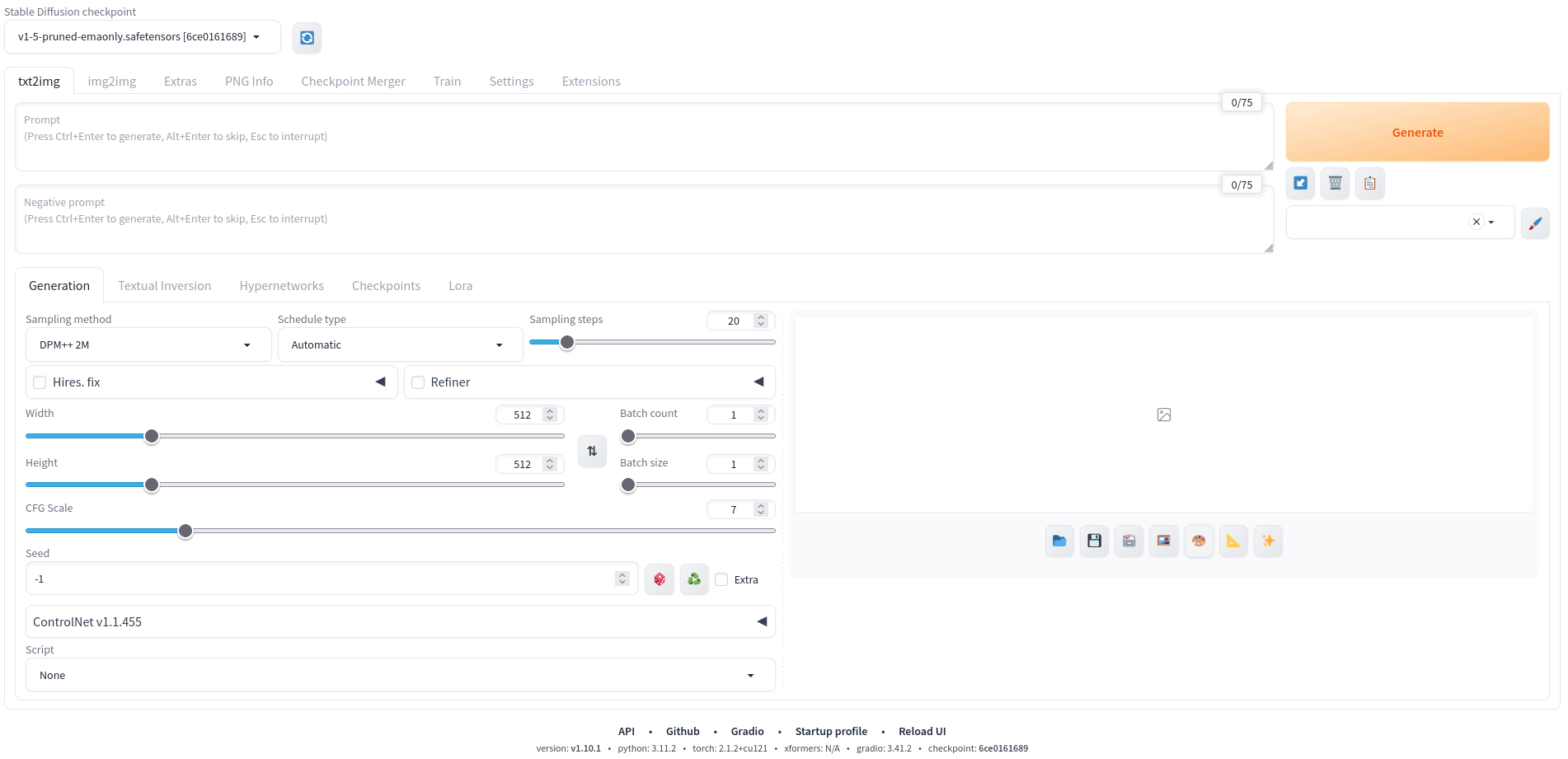
Figure 4. Capture d’écran de l’interface Automatic1111
1.3 ) ControlNet
Pour créer des images avec en entrée une autre image (nos illusions de Kanizsa par exemple, voir annexe 2. Images d’entrée ControlNet) nous devons utiliser l’extension ControlNet.
ControlNet est un module complémentaire pour les modèles de diffusion comme Stable Diffusion qui permet de copier des compositions d’image à partir d'une image de référence. ControlNet est donc bien plus qu'un simple outil d'image-to-image.
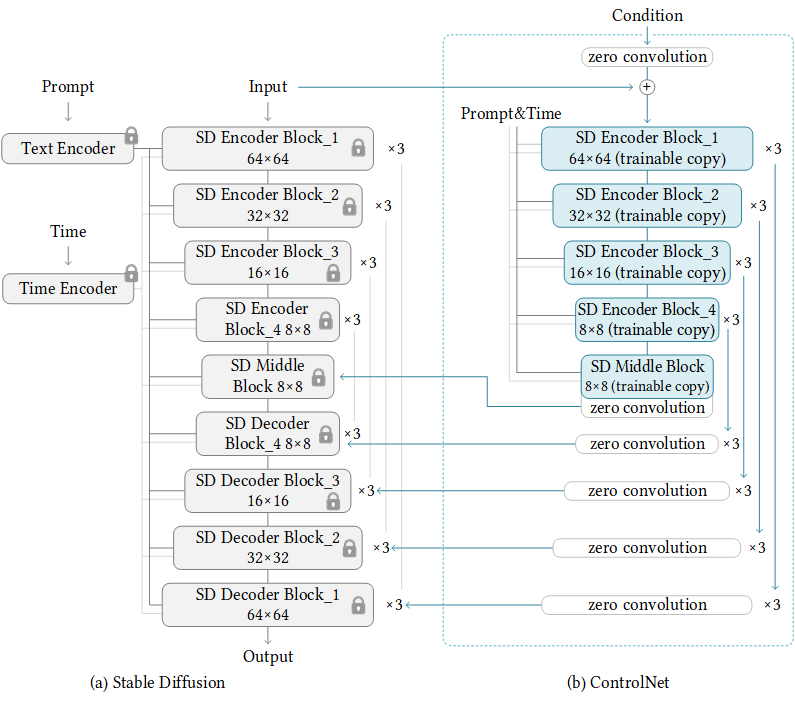
Figure 5. Structure du modèle de ControlNet
Le modèle de Controlnet reprend la structure de l’U-Net du modèle de diffusion, puis vient se greffer sur la seconde partie de l’U-Net, celle correspondant au “Decoder” [7]. Au moment de générer l’image à partir de bruit, ControlNet va en quelque sorte “guider” les choix de la génération, en réintroduisant l’image d’entrée à chaque couche. Cela permet de s’assurer que les informations de l'image d’entrée soient bien présentes dans l’image finale, et localisées au bon endroit.
ControlNet offre une grande précision, permettant aux utilisateurs de choisir les éléments de l'image d'origine qu'ils souhaitent conserver ou ignorer. Il s'intègre donc parfaitement avec des interfaces comme Automatic1111 pour offrir un contrôle précis et avancé sur le processus de génération d'images, notamment via les hyperparamètres du modèle.
Voici la liste des hyperparamètres de ControlNet (Figure 6) est la suivante :
- Le control weight : son rôle est d’influencer ControlNet sur l’image finale. 1 étant l’influence maximale et 0 signifie que ControlNet est ignoré. Plus on le réduit et plus on laisse de liberté au prompt.
- Le starting control step : correspond à l’étape du sampling à partir de laquelle ControlNet commence à agir.
- Le ending control step : correspond à l’étape où ControlNet arrête d’agir. Par exemple de 0 à 1, ControlNet agit du début à la fin, et de 0.2 à 0.8 ControlNet agit partiellement.
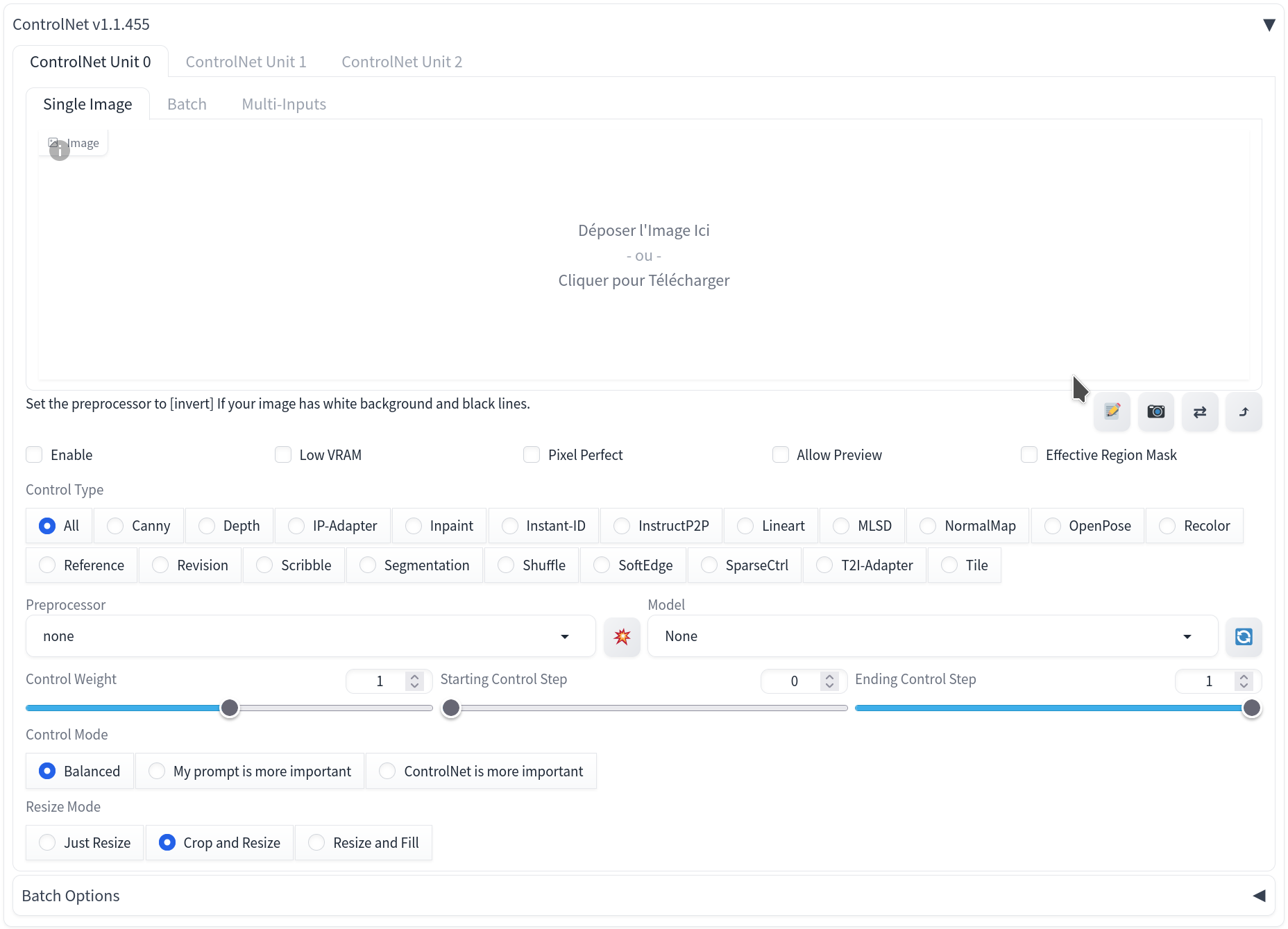
Figure 6. Onglet ControlNet présent dans Automatic1111
1.4 ) Génération des images
a ) L'interface choisie
Dans la partie précédente, nous avons expliqué comment fonctionne un modèle de diffusion. Maintenant, nous allons motiver notre choix de la WebUI Automatic1111.
Automatic1111 est une WebUI, comprenez Web User Interface, c’est-à-dire une interface utilisateur basée sur le web qui permet aux utilisateurs d'interagir avec une application ou un service via un navigateur internet. Automatic1111 a la particularité d’être facile d’installation et d’utilisation (si votre machine a la puissance de calcul nécessaire) et nous permet, après avoir choisi notre modèle de diffusion, de générer une image ou une série d’images correspondant aux paramètres et hyperparamètres souhaités.
C’est donc sa facilité de prise en main et les conseils de nos encadrants qui nous ont poussé à choisir Automatic1111 pour générer nos images.
Automatic1111 est principalement conçu pour StableDiffusion qui est un modèle de diffusion open-source. Nous avons donc utilisé la version “v1-5-pruned-emaonly.safetensors” de ce modèle.
Il existe beaucoup de versions de StableDiffusion, et surtout, il en existe des plus récentes. Néanmoins, l’utilisation d’extensions avancées comme ControlNet nécessite un matériel informatique puissant. Pour obtenir des performances fluides, il est recommandé de disposer d'une carte graphique NVIDIA avec au moins 6 à 8 Go de mémoire VRAM. À titre d’exemple, la génération d’une seule image 512x512 avec ControlNet peut mobiliser jusqu’à 8–12 Go de VRAM, ce qui dépasse les capacités des GPU intégrés aux ordinateurs portables classiques. Nous avons donc choisi une version plus ancienne (la v1-5) mais accessible et suffisante pour produire des résultats pertinents tout en restant compatible avec notre matériel.
Pourquoi choisir ce modèle en particulier ?
“pruned” signifie que certaines parties moins importantes du modèle ont été supprimées pour réduire sa taille et améliorer son efficacité sans sacrifier trop de performance.
“emaonly” sous-entend “seulement EMA” qui signifie “Exponential Moving Average” (Moyenne Mobile Exponentielle). C'est une technique utilisée pour améliorer la stabilité et la performance des modèles d'apprentissage automatiques. Les poids EMA sont souvent utilisés pendant l'entraînement pour obtenir une version plus stable du modèle, qui généralise mieux les données non vues.
Le format “.safetensors” est plus adapté dans les cas avec des contraintes matérielles, que le format plus classique “.ckpt”. En effet, l’avantage principal de “.ckpt” est qu’il permet, dans un environnement où la sécurité n’est pas prioritaire, de modifier plus facilement les poids du modèle. Or nos recherches n’allant pas jusqu’à la modification de la structure des modèles, le format ".safetensors” était tout à fait adapté à notre usage.
Toutes ces propriétés ont donc justifié le choix de ce modèle précis.
b ) Le code python
Comme vu précédemment, la génération d’images avec StableDiffusion via l’interface Automatic1111 est simple. Malheureusement une contrainte majeure nous a quelque peu ralenti : Automatic1111 ne permet pas la génération d’une série d'images de paramètres différents, c'est-à-dire que pour générer 5 images de weight différents, il faut créer chaque image en changeant manuellement le weight. Or, nos expériences et nos tests ont nécessité la génération de plus de 1000 images, ce qui, assez logiquement, nécessite une automatisation. C’est pourquoi, nous avons décidé de créer une boucle python nous permettant très simplement de concevoir des images.
Pour cela, nous avons automatisé la génération d’images en utilisant l’API d’Automatic1111. Concrètement, nous avons lancé l’interface, depuis le terminal linux, avec l’option --api, ce qui permet à un script Python d’envoyer automatiquement des requêtes avec des prompts et des paramètres. Ce script interagit avec le serveur comme si nous passions manuellement par l’interface, mais tout se fait sans intervention humaine, ce qui permet de générer des images en boucle. Ainsi les images n’avaient plus qu’à être stockées selon leurs propriétés et nous pouvions commencer les expériences.
2 ) Les illusions de type Kanizsa
2.1 ) Théorie de la Gestalt
La psychologie de la forme, ou théorie de la Gestalt, vient du Gestaltisme, un courant de la psychologie cognitive de la première partie du XXème siècle. Cette théorie explique que les processus de la perception et de la représentation mentale traitent les phénomènes comme des formes globales plutôt que l’addition d’éléments simples.
Un principe important de cette théorie est le suivant : “Le tout est différent de la somme des parties”. La structuration des formes ne se fait pas au hasard, mais notre perception est soumise à un certain nombre de lois. Par exemple, la loi de la bonne forme (Figure 7), qui est une des lois principales de la Gestalt, est un ensemble de parties informes (comme des groupements aléatoires de points) qui est d’abord perçu comme une forme simple, stable et familière. Sur la Figure 7, nous voyons soit un vase soit deux visages de profil, mais pas les deux en même temps.

Figure 7. Vase de Rubin, qui représente la loi de la bonne forme
Deux autres sont la loi de la proximité (Figure 8) selon laquelle nous regroupons d’abord les points les plus proches les uns des autres et la loi de similarité (Figure 9) qui explique que si la distance ne permet pas de regrouper les points, nous nous attacherons ensuite à repérer les plus similaires entre eux pour percevoir une forme. Ces lois agissent en même temps et sont parfois contradictoires.

Figure 8. Loi de proximité

Figure 9. Loi de similarité
Durant ce courant de psychologie cognitive, une illusion d’optique est publiée en 1955 par Gaetano Kanizsa. C’est le motif de Kanizsa (Figure 10). Cette illusion s’appuie sur les reliefs des formes dîtes de “pac-man” et des traits noirs en forme de triangle pour former une forme imaginaire (ici un triangle) qui semble cacher les autres figures (les ronds noirs et le triangle noir). Autrement dit notre cerveau nous fait croire qu’on perçoit un triangle blanc dont le tracé n’existe pas.
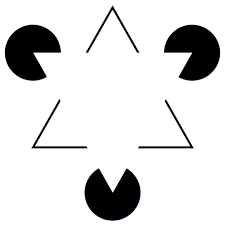
Figure 10. Motif de Kanizsa
D’autres formes ont été publiées par la suite mais nous nous intéresserons seulement, dans ce mémoire, aux “pac-man” qui forment des quadrilatères. Nous nous référons donc à la figure suivante :

Figure 11. Illusion du carré de Kanizsa
2.2 ) Interprétations en psychologie cognitive
Pour comprendre comment fonctionnent la vision et la perception dans le cas d’une illusion de Kanizsa, nous allons définir les différentes aires du cortex visuel.
Le cortex visuel primaire, noté V1, reçoit en premier les informations venant de la rétine et du corps genouillé latéral.
Le cortex visuel secondaire, noté V2, reçoit les informations du cortex visuel primaire. Le cortex visuel secondaire envoie ensuite les informations à d’autres zones du cerveau à travers deux voies :
- La voie ventrale qui gère les informations liées aux formes et aux couleurs, elle conduit vers les aires corticales V3 et V4 sont respectivement spécialisées dans les formes et les couleurs.
- La voie dorsale qui gère les informations liées aux mouvements et positions dans l’espace, elle conduit vers l’aire corticale V5 qui gère les mouvements.
V2 opère un triage des sorties de V1 vers les aires spécialisées, appelées aires visuelles associatives, telles que V3, V4 et V5 (Kartable [3]). Voir la figure suivante :
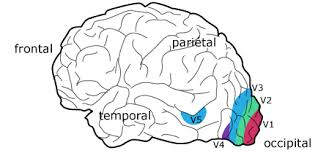
Figure 12. Aires visuelles dans le cortex
La question fondamentale que se posent tous les chercheurs étudiant la vision : "comment les aires spécialisées interagissent-elles pour fournir une image intégrée, unifiée du monde ?"
Semir Zeki, un biologiste franco-anglais, suggère qu’un rôle important est joué par les connexions rétroactives (des aires d’aboutissement vers les aires d’émission des messages) pour l’intégration des informations visuelles dans le cortex, et donc l’unification de la vision du monde (Faïta [4]).
Pour illustrer ce rôle, voici un exemple : la perception des contours illusoires du motif de Kanizsa.
Dans cette illusion, on a l'impression de voir un triangle blanc, alors qu’en réalité, il n’est pas dessiné. Ce sont juste trois cercles ouverts et quelques formes noires qui donnent cette impression.
Des chercheurs ont enregistré l’activité des neurones dans la zone V1 du cerveau (la première zone qui traite l’image). Ils ont vu que les neurones situés là où devrait se trouver le triangle ne réagissent pas, car il n’y a rien de réellement dessiné à cet endroit. En revanche, les neurones de la zone V2 (qui reçoivent les informations de V1) s’activent. Ils ont des champs récepteurs plus grands qui leur permettent d’analyser des zones plus larges de l’image et de repérer des formes plus complexes. Ils "devinent" qu’il y a un triangle, même s’il n’est pas vraiment là. Les chercheurs pensent que cette illusion est possible grâce à des connexions en retour venant de la zone V4 vers la zone V2. Ce sont des connexions dîtes rétroactives. Elles aident le cerveau à compléter l’image en fonction de ce qu’il "s’attend" à voir.
Finalement, le système de rétroaction peut avoir 3 fonctions simultanées :
- Unifier les signaux de forme trouvés en V4 ;
- Envoyer les informations de formes complètes en V4 vers des aires à cartes topographiques précises en V2 ;
- Intégrer des informations de forme dans une autre aire “sous-jacente”.
Ainsi, le système rétroactif peut participer à l’unification des signaux issus de l’analyse des différents paramètres des stimuli visuels qui nous entourent (Delacour, 2001 [5]).
3 ) Lien entre modèle de diffusion et illusion d’optique
Les modèles de diffusion et les illusions d’optique partagent une notion fondamentale : le fait de compléter les informations manquantes à partir d’éléments partiels ou ambigus.
D’un côté, les modèles de diffusion apprennent à reconstruire une image à partir d’un bruit progressif. Ce processus de débruitage, appris par le réseau, permet au modèle de générer une image réaliste sans avoir accès à une image de référence. Le modèle ne "copie" pas, il devine et apprend, étape après étape, une configuration visuelle plausible en s'appuyant sur des régularités et des similarités.
De l’autre côté, les illusions de type Kanizsa reposent sur un mécanisme similaire, mais chez l’humain, le cerveau complète des formes absentes à partir d’indices partiels, en s’appuyant sur des lois perceptives (Gestalt, rétroaction corticale, etc…) et des connexions rétroactives entre les aires visuelles du cortex. L’illusion résulte donc d’un remplissage perceptif, souvent inconscient, qui transforme des éléments fragmentés en une forme perçue complète.
Ces deux mécanismes, génératif chez la machine et perceptif chez l’humain, suggèrent un parallèle conceptuel : la capacité à reconstruire une forme entière à partir de fragments. C’est ce point commun qui fonde notre interrogation principale : “Les modèles de diffusion, en apprenant à générer des images cohérentes à partir du bruit, peuvent-ils eux aussi faire apparaître spontanément des illusions visuelles telles que celles de Kanizsa ?”
Si tel est le cas, cela signifierait que les modèles ont, en quelque sorte, intégré des régularités perceptives similaires à celles du système visuel humain, non pas par compréhension, mais par entraînement sur de vastes jeux d’images.
Cette interrogation constitue le point de bascule entre notre étude théorique et notre expérimentation. C’est à partir de ce lien conceptuel que nous avons construit notre problématique et notre protocole expérimental, en testant si les IA génératives peuvent produire, sans supervision explicite, des images porteuses d’illusions perceptives similaires à celles que perçoit l’humain.
II ) DEUXIÈME PARTIE - QUESTION DE RECHERCHE
1 ) Convergence vers la problématique
Le sujet à l’origine de notre recherche est
- Un modèle de diffusion perçoit-il, dans le même sens que l’humain, les illusions de type Kanizsa ?
- Un modèle de diffusion peut-il générer des illusions de type Kanizsa dans un environnement écologique ?
- Des personnes peuvent-elles percevoir des illusions de type Kanizsa dans un environnement écologique généré par un modèle de diffusion ?
Tout d’abord, notre réflexion s'est portée sur le questionnement de la perception des illusions de Kanizsa par le modèle de diffusion. Dans la partie 2.2, nous avons vu que les illusions de Kanizsa consistaient à induire la présence de formes alors que leurs côtés ne sont pas tracés. Ainsi nous pouvions nous attendre à ce qu’un modèle de diffusion se fasse également tromper sur la présence de lignes inexistantes.
Une vérification simple pour répondre à cette question consistait à créer un grand nombre d’images (voir 3. Série d'images 1) avec une illusion de Kanizsa dans le ControlNet et d’analyser si une part non-négligeable des images générées contenait une interprétation entière de la forme de l’illusion de Kanizsa, c'est-à-dire dans lesquelles on peut distinguer clairement les lignes qui complètent les formes illusoires.
Nous avons donc généré plusieures centaines d’images avec des hyperparamètres variés (2 prompts, 3 samplers, une grande plage de weight ControlNet …) et une illusion carrée de Kanizsa (Figure 11).
Il se trouve que seulement 3 ou 4 images sur les centaines générées représentent bien les côtés de la forme de Kanizsa.

Figure 13. Image particulière pour laquelle les côtés du carré sont tracés
À la problématique "un modèle de diffusion perçoit-il, dans le même sens que l’humain, les illusions de type Kanizsa ?", nous pouvons donc répondre non.
La deuxième problématique qui était “Un modèle de diffusion peut-il générer des illusions de type Kanizsa dans un environnement écologique ?” est en partie déjà résolue. En effet, l'expérience précédente nous prouve qu'effectivement, un modèle de diffusion peut générer des illusions de type Kanizsa. Néanmoins il n’était pas encore question de réalisme ! Pourquoi avons-nous eu l’idée de chercher à modéliser des illusions dans un environnement écologique ? Tout d’abord, précisons que visualiser des images n’est pas à proprement parler “écologique” mais que dans le cadre de notre étude, le but est justement de tendre vers cette notion d’environnement écologique. Nous parlerons donc dans le reste de ce rapport d’environnement écologique tout en gardant cette précision en mémoire.
L’idée nous vient de l’illusion de Müller-Lyer. En effet, cette dernière a la particularité de pouvoir être observée grâce à l’architecture des bâtiments.
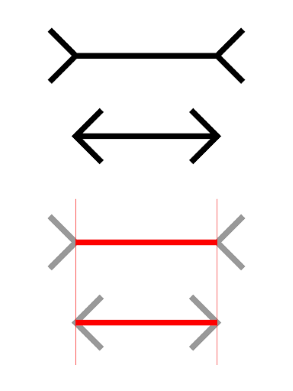
Figure 14. Illusion de Müller-Lyer
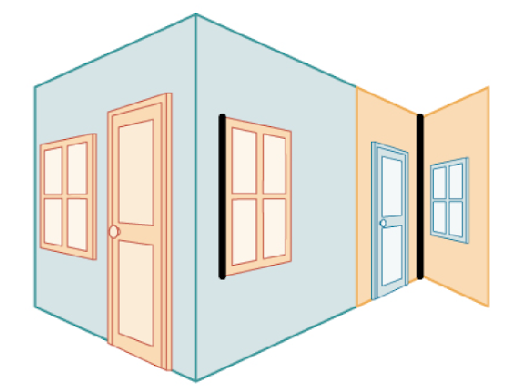
Figure 15. Perception de l’illusion de Müller-Lyer dans un environnement
Le but est donc dorénavant d’étudier les hyperparamètres de notre modèle de diffusions et de générer des images combinant un bon réalisme et une bonne visibilité de l’illusion de Kanizsa. Nous avons donc créé une expérience dont nous sommes les seuls participants.
Nous avons construit un protocole simple, nous permettant de choisir les hyperparamètres clefs dans la génération d’image.
Sur JupyterLab, nous nous sommes présenté 229 images (voir 4. Série d'images 2) une à une. Pour chaque image présentée, deux questions étaient posées : “Combien mettez-vous en note de réalisme ? (0-10)” et “Combien mettez-vous en note d’illusion ? (0-10)”. Pour une personne ne travaillant pas sur le projet depuis plusieurs mois, ces questions peuvent sembler inappropriées et mal formulées. En réalité, ces questions nous étaient directement destinées, nous en comprenions donc l’entièreté du sens.
Avant de donner les résultats de cette mini-expérience, il est bon de préciser quels hyperparamètres étaient ajustés pour notre jet d’images :
- Le prompt : nous avions deux prompts relativement similaires et complets
- Le sampler : nous avons testé “Euler a” et “DPM++ 2M Karras”
- Les steps : 40, 80, 100 et 120
- Le weight ControlNet : 0, 0.2, 0.4, 0.6, 0.9, 0.925, 0.95, 0.975, 1, 1.025, ... , 1.2, 1.4
L’image dans le ControlNet était une illusion carrée de Kanizsa (Figure 11) et elle était toujours située au milieu.
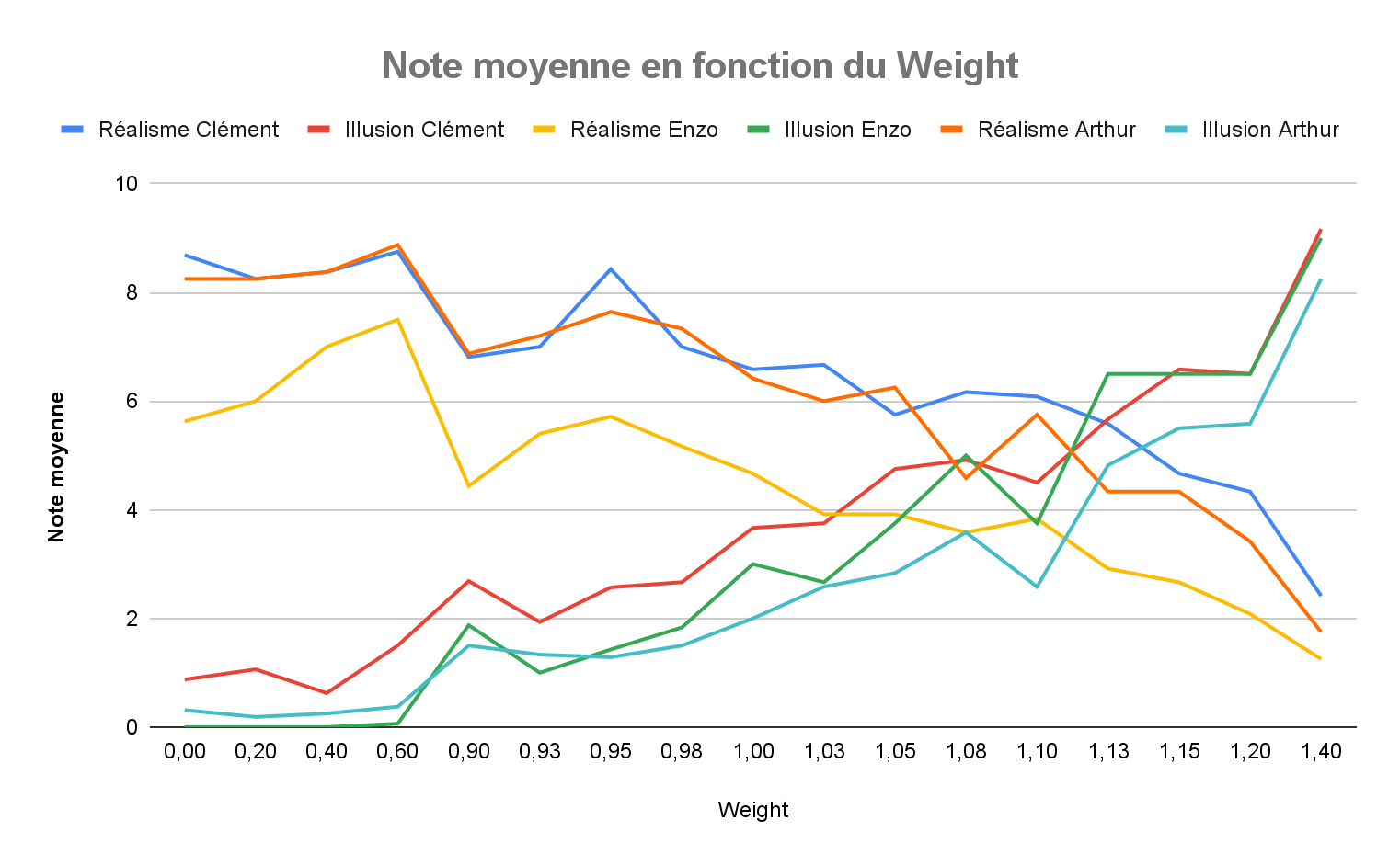
Figure 16. Graphe des moyennes de réalisme et visibilité de l’illusion des participants en fonction du weight
La figure 16 montre une corrélation négative entre réalisme et visibilité de l’illusion lorsque le weight de ControlNet augmente : ce résultat semble logique au vu de la définition du weight de ControlNet (voir partie 1.3 ControlNet). En effet, plus ce dernier est élevé, plus le modèle de diffusion cherchera à mettre l’image de ControlNet en évidence. De plus, ce graphe met en évidence la plage de weight qui maximise à la fois le réalisme et la visibilité de l’illusion [1.05, 1.15].


Figure 17. Images ayant les mêmes paramètres mis à part le weight qui est de 0.4 à gauche et de 1.4 à droite
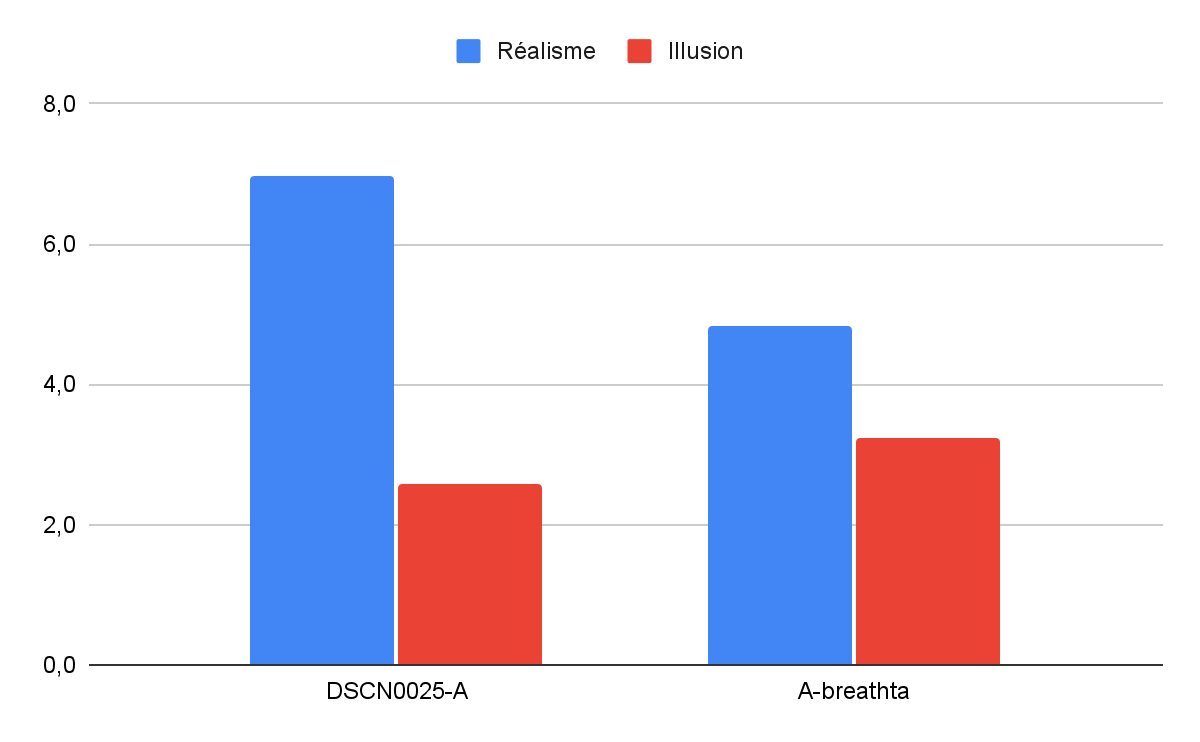
Figure 18. Histogramme des moyennes de réalisme et de visibilité de l’illusion par prompt

Figure 19. Prompt 1

Figure 20. Prompt 2
D’après la figure 19, le prompt 1 semble être meilleur que le prompt 2 car il a une moyenne de réalisme bien plus élevée pour une note d’illusion légèrement plus faible. Cela doit être dû à la seule différence entre ces deux prompts : la présence multiple de “DSCN0025” dans le prompt 1. “DSCN” signifie “Digital Still Camera Nikon” (le 0025 dit juste la 25e image) ; en fait cet argument sert à pousser le modèle de diffusion à reconstruire l’image de la même manière que les images d'entraînement prises avec un appareil photo Nikon.
En effet, dans la large base de données qui a servi à entraîner les modèles, les images ayant ce nom ont été directement extraites d’un appareil photo. Cela permet donc de rapprocher l’image générée du réalisme recherché.
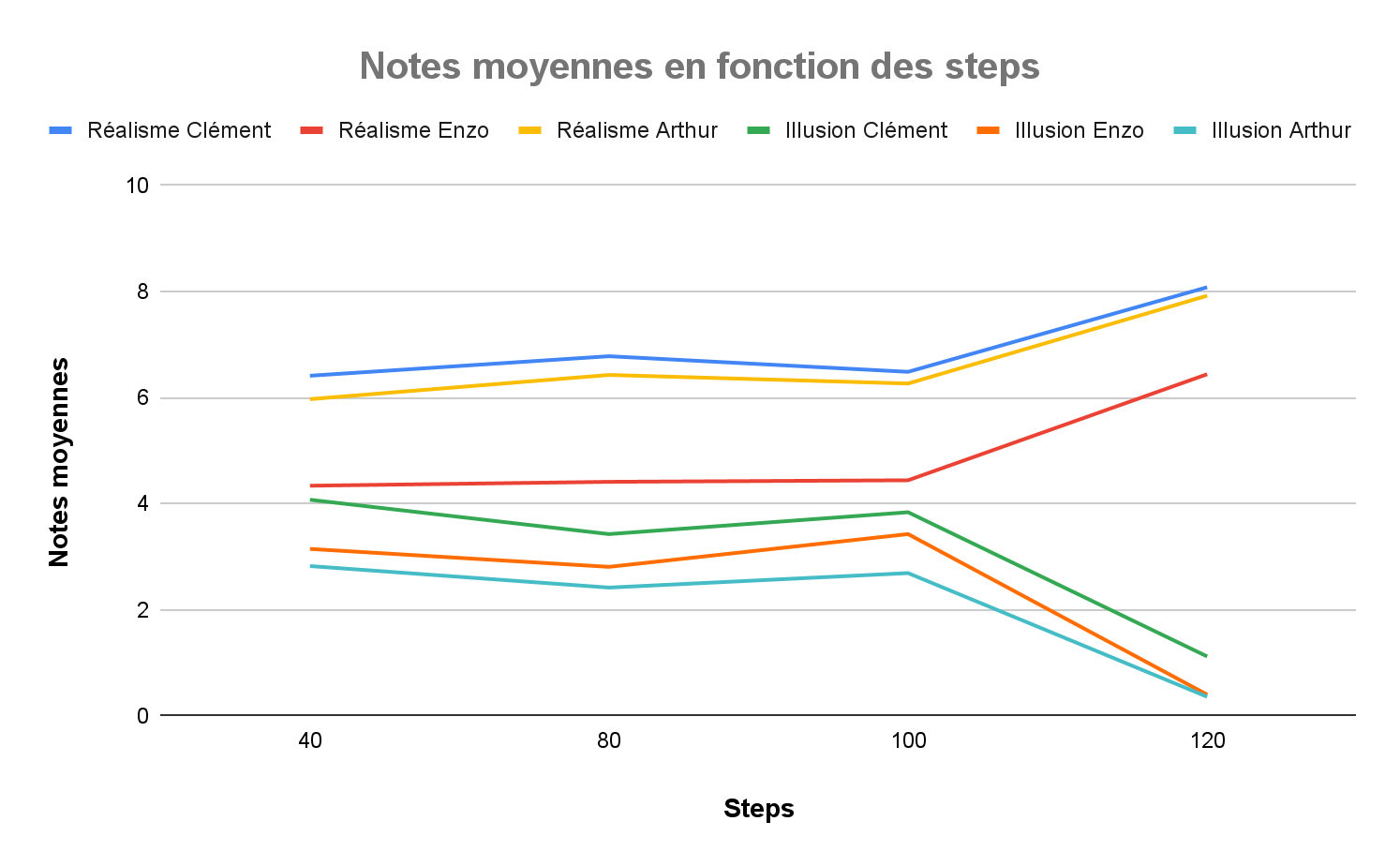
Figure 21. Graphe des moyennes de réalisme et de visibilité d’illusion des participant en fonction du steps
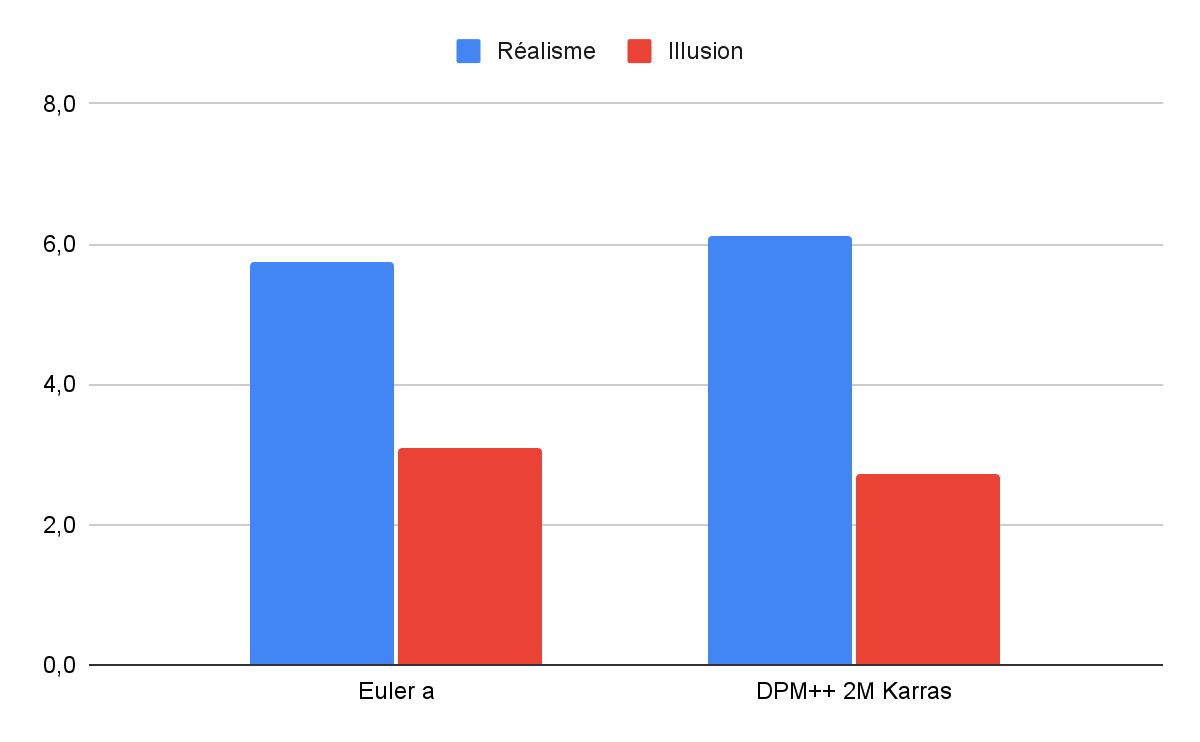
Figure 22. Histogramme des moyennes de réalisme et de visibilité de l’illusion par sampler
Augmenter le nombre de steps, augmente la finesse de l’image générée. Or la figure 21 indique une valeur limite, steps = 100, au-delà de laquelle le réalisme augmente fortement mais au dépend de la visibilité de l’illusion qui chute drastiquement. Ainsi, le choix d’un steps proche mais inférieur à 100 semble être la meilleure option.
De même, nous avons choisi le sampler “DPM++ 2M Karras” car sa note moyenne de réalisme était légèrement plus élevée. Les différences d’évaluations entre les deux sampler étant minimes, il convient de préciser que ce choix est relativement arbitraire.
Ainsi la présence d'images comme celle de la figure 23 nous aide à répondre à la question : “Un modèle de diffusion peut-il générer des illusions de type Kanizsa dans un environnement écologique ?”.
La réponse est : oui dans une certaine mesure, un modèle de diffusion en est capable si l’on choisit les bons paramètres.

Figure 23. Image ayant à la fois une bonne moyenne de réalisme et de visibilité de l’illusion
La réponse à la problématique précédente nous permet donc de nous poser la problématique majeure de notre étude : “Des personnes peuvent-elles percevoir des illusions de type Kanizsa dans un environnement écologique généré par un modèle de diffusion ?”.
2 ) Protocole de l'expérience
Notre hypothèse est la suivante : “Les personnes peuvent percevoir des illusions de type Kanizsa dans un environnement écologique généré par un modèle de diffusion”. Nous avons donc structuré une expérience pour tenter de confirmer ou d’infirmer notre hypothèse.
L’expérience consiste à regarder 48 images pendant un certain temps puis répondre à une série de questions. Tous les participants voient les mêmes 48 images mais celles-ci sont affichées de façon aléatoire. Chaque image est affichée pendant 10 secondes, puis une fois que ce temps est écoulé, elle disparaît et les questions s’affichent. L’objectif est de contrôler le temps d’observation de l’image pour qu’il soit identique pour chaque participant. Dans un premier temps, deux questions sont affichées :
Question 1 : “A quel point l’image est-elle réaliste ?”
Question 2 : “Voyez-vous un quadrilatère dans cette image ?”
Nous avons choisi de répondre à la question 1 par une échelle quantitative de 0 à 10 plutôt qu'une échelle qualitative telle que : Pas du tout / Un peu / Moyennement / Plutôt / Tout à fait réaliste. Les nombres permettent une analyse plus fine des réponses ainsi qu’une uniformisation de la quantification de l’échelle.
La question 2 nous permet d’attirer l’attention des participants sur la recherche de quadrilatère dans l’image afin de les guider et de répondre à l’hypothèse formulée. Les participants peuvent répondre à la question 2 par : Oui ou Non. Si la réponse est Oui, trois autres questions apparaissent :
Question 3 : “De quel quadrilatère s’agit-il ?”
Question 4 : “Où est situé ce quadrilatère dans l'image ?”
Question 5 : “Avec quelle certitude avez-vous perçu ce quadrilatère ?”
Les réponses aux questions 3 et 4 sont des cases à cocher avec un texte associé afin de faciliter la compréhension des participants et de réduire le temps de réponse plutôt que d’écrire en toutes lettres. Pour la question 5 c’est une réponse graduelle entre 0 et 10. L’objectif de ces questions est de savoir si les participants voient bien la forme et la localisent au bon endroit dans l’image, cela permet de limiter les faux positifs.
Pour faire passer l’expérience aux participants, nous nous servons de notre site web, dont la conception est détaillée à la prochaine partie. Pour voir la page de l'expérience ainsi que les consignes vous pouvez cliquer ici.
Les consignes expliquent le déroulement de l’expérience, l’objectif que doivent atteindre les participants, ainsi que des exemples de quadrilatères qui seront présents dans l’expérience et qu’il faudra repérer. Ces formes géométriques sont affichées en image et en texte dans les consignes pour que tout le monde ait la même définition de ces dernières. Le choix des quadrilatères vient du fait que nous souhaitions avoir le même nombre d’éléments inductifs, ici 4 pour chaque “pac-man”, et pouvoir avoir plusieurs formes au lieu d’un unique carré par exemple. Les quadrilatères choisis sont le carré, le losange et le parallélogramme (voir les images d'entrée de ControlNet).
Les localisations des quadrilatères dans l’image sont : 1 pour en haut à gauche, 2 en haut à droite, 3 en bas à gauche, 4 en bas à droite et 5 au milieu. Placer les quadrilatères à des localisations différentes permet de limiter les faux positifs. L’objectif est d’être certains que les participants voient le bon quadrilatère au bon endroit. Le weight lui, prend les valeurs 1, 1.05 ou 1.1, comme vu dans la partie précédente sur l’optimisation des hyperparamètres. Après avoir répondu aux questions, les participants appuient sur le bouton “Suivant” et l’opération se renouvelle.
Parmi les 48 images présentées, 3 sont des images contrôle. C’est-à-dire qu’elles ne contiennent pas d’illusions de Kanizsa. Elles ont été générées de la même manière que les autres images, à la seule différence que l’image d’entrée n’était pas une illusion mais une image entièrement blanche. Il y en a trois pour chaque poids différents (1, 1.05 et 1.1). Nous avons donc généré les images contrôle pour qu’il y en ait autant que de chaque autres images d’entrée.
Les variables indépendantes (manipulées) sont l’image de base et sa transformation. Les variables dépendantes (mesurées) sont les réponses des participants aux questions posées.
Nous nous attendons notamment à ce que les notes de réalisme soient plutôt élevées (avec une moyenne supérieure ou égale à 5) et que les formes soient globalement bien perçues (avec un pourcentage supérieur ou égal à 50% de vrais positifs).
III ) TROISIÈME PARTIE - PASSATION ET ANALYSE DES DONNÉES
1 ) Conception du site web
L’objectif de créer un site web était de rendre accessible l’expérience au plus grand nombre. Le problème étant les biais que cela pourrait potentiellement engendrer. Tout le monde ne réalise pas l’expérience dans les mêmes conditions expérimentales. C’est pour cela que nous avons fait en sorte de les limiter en précisant que la passation se fait uniquement sur ordinateur, en mettant le site en plein écran et en passant le site en mode clair peu importe le moteur de recherche ou le système d’exploitation utilisé et de bien avoir lu les consignes. Nous avons, pour cela, codé en HTML, php et JavaScript la page “experience.html” qui présente cela.
Une fois l’expérience lancée, la page du site passe en plein écran pour éviter toute distraction visuelle, empêcher les personnes de quitter la page et faciliter la concentration pendant toute la durée de l’expérience. Le mode clair s’active pour tout le monde, ce qui permet d’obtenir un affichage équivalent pour tous, et d’améliorer la visibilité des images.
En ce qui concerne les données des participants, quand l’expérience se lance, on attribue un identifiant aléatoire à chaque personne. Comme expliqué dans la partie précédente, les participants répondent à une série de questions pour chaque image présentée. Chaque nouvelle image et leurs questions associées apparaissent sur une nouvelle page. Les réponses aux questions sont obligatoires, ce qui permet d’éviter les erreurs et de passer aux questions suivantes sans avoir répondu.
Le code JavaScript de la page “exp.php” nous permet donc de sauvegarder les réponses et de savoir à quelle image cela correspond grâce à l’identifiant de l’image. A la fin de l’expérience, quand les sujets appuient sur le bouton “Terminer et envoyer”, le code PHP enregistre les réponses dans un fichier csv avec en colonnes l’identifiant de l’image, la réponse à la question 1, puis la question 2, etc jusqu’à la question 5. Nous avons donc un fichier par participant regroupé dans un dossier “data”.
Concernant le choix de la forme des réponses aux questions, nous avons opté pour des réponses faciles à comprendre. Nous avons donc exclu la possibilité de répondre librement en écrivant un texte. Les réponses sont des cases à cocher dont les informations sont pré-remplies pour que les participants aient simplement à lire et cocher la réponse qui semble correspondre au mieux à la question posée. Pour le choix du slider (échelle de 1 à 10), nous voulions que les participants aient uniquement à cliquer sur un bouton et le bouger pour atteindre la valeur qu'ils souhaitaient mettre. Le problème que nous avons rencontré lors de l’analyse des données est que certaines personnes ne touchaient pas le slider, ce qui laissait une réponse de 5/10 à chaque question. Nous aurions pu opter, à la place, pour une échelle qui de n’a aucune valeur initiale et une fois appuyé sur un bouton augmente ou diminue au souhait du participant. Cette réponse aurait été obligatoire et nous aurait évité des réponses identiques pour certains participants qui ont oublié de bouger le slider ou n’ont pas eu envie de le faire.
2 ) Analyse de nos résultats
2.1 ) Outils pour l'analyse
Dans cette partie, nous avons regroupé les analyses que nous avons faites sur les 128 participants qui ont effectué l’expérience. Cela a nécessité quelques outils statistiques que nous allons présenter dans cette sous-partie. Nous tenons à préciser que l’intégralité des analyses ont été faites sous RStudio et que la beauté des graphes est due à l’installation de nombreux packages.
Le calcul de moyenne est probablement le calcul qui nous a le plus servi mais un problème s’est vite posé : “comment calculer une note fiable pour chaque image sans que quelques participants très sûrs d’eux faussent les résultats ?”
Nous souhaitions éviter qu’un petit nombre de participants très confiants n’exerce une influence excessive sur la moyenne d’évaluation d’une image. En effet, si seules quelques personnes attribuent une note de confiance élevée à une illusion, cela ne suffit pas à en valider la perception de manière fiable. Pour limiter cet effet et mieux prendre en compte la taille des échantillons, nous avons utilisé une moyenne pondérée inspirée de la méthode IMDb. Cette formule, issue du système de notation utilisé par le site de référence IMDb (Internet Movie Database), permet d’atténuer l’impact des résultats obtenus sur de faibles effectifs en pondérant la note finale selon le nombre de notes attribuées.
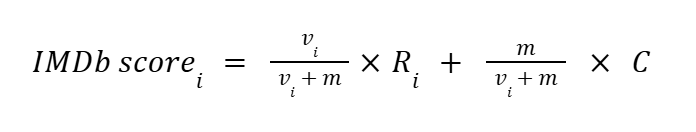
Dans notre cas, la moyenne IMDb est une moyenne de confiance, vi représente le nombre de participant ayant la bonne réponse pour l’image i, m est la médiane du nombre de notes de confiance par image, Ri la moyenne des notes de confiance pour l’image i et C est la moyenne globale des notes de confiance.
2.2 ) Paysage des données
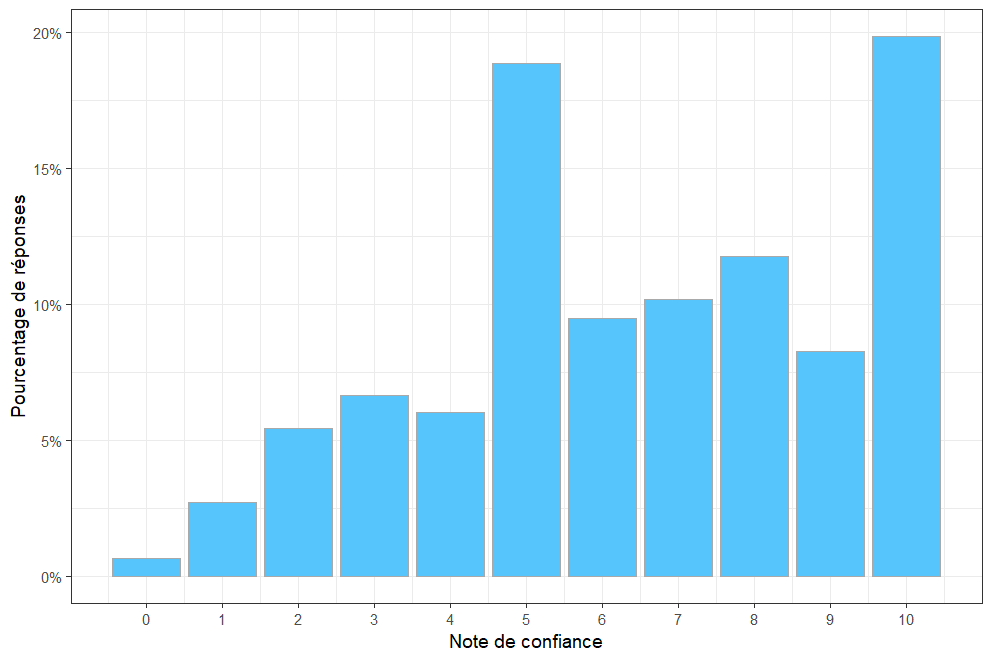
Figure 24. Histogramme de la répartition des notes de certitude de perception
Nous observons sur cet histogramme la surreprésentation des 5 qui est fort probablement due à la valeur initiale des sliders utilisés sur le site web pour noter les images.
Figure 25. Slider présent dans l’expérience
Une solution pour remédier à ce problème aurait été de mettre pour valeur initiale -1, ainsi nous aurions pu trancher entre un un slider non utilisé et un 5. Nous aurions également pu utiliser une boîte textuelle plus classique, obligeant chaque participant à saisir manuellement une note. Cette deuxième solution avait été écartée au moment de la construction du site car nous la jugions trop peu ergonomique.
Nous remarquons également le très faible nombre de 0, qui paraît logique étant donné que les participants ont accès à cette note seulement s’ils disent avoir perçu une forme.
Enfin, à l'opposé de l’échelle, le très grand nombre de 10 indique que pour beaucoup de participants, lorsqu'ils ont indiqué avoir perçu une forme, ils en étaient absolument certains.
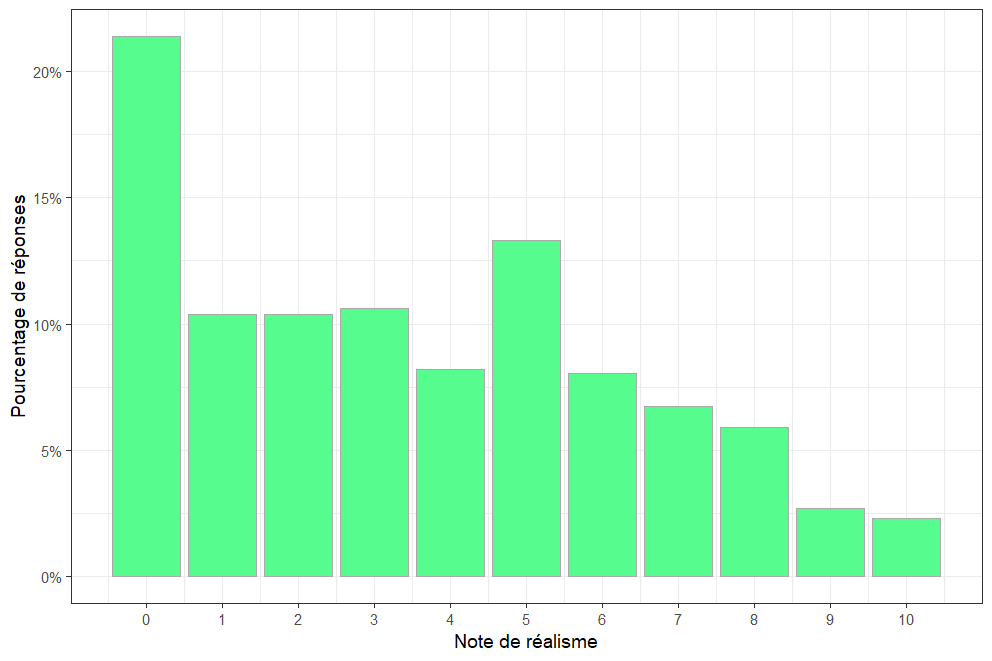
Figure 26. Histogramme de la répartition des notes de réalisme
De la même manière que pour les notes de confiance, on observe un grand nombre de 5. Les autres notes ne semblent, de prime abord, pas sujettes à de quelconques biais.
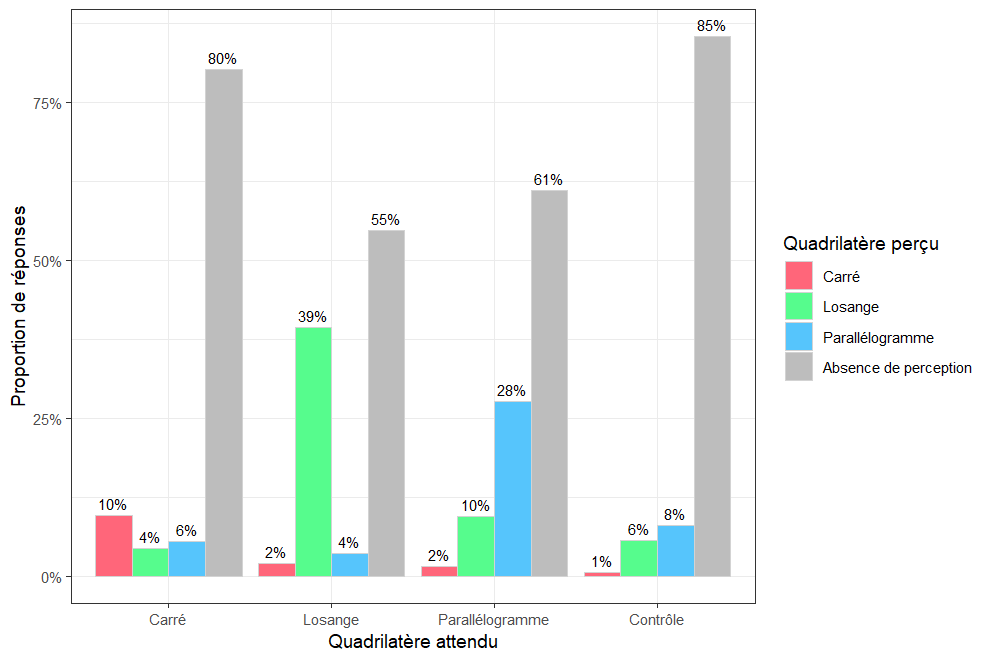
Figure 27. Histogramme de la répartition des quadrilatères perçus
Sur la figure 27 nous observons le grand nombre d’absence de perception de quadrilatère. Il en découle deux possibilités : soit les participants n’arrivent pas à percevoir la forme, soit les formes sont trop difficiles à percevoir.
Lorsque les participants disent avoir reconnu un losange, il s’agit du bon losange dans 32% des cas. Cela signifie que certaines des formes sont bien perceptibles.
Nous pouvons mieux nous représenter le nombre de reconnaissances de forme, au bon endroit, avec l'histogramme suivant :
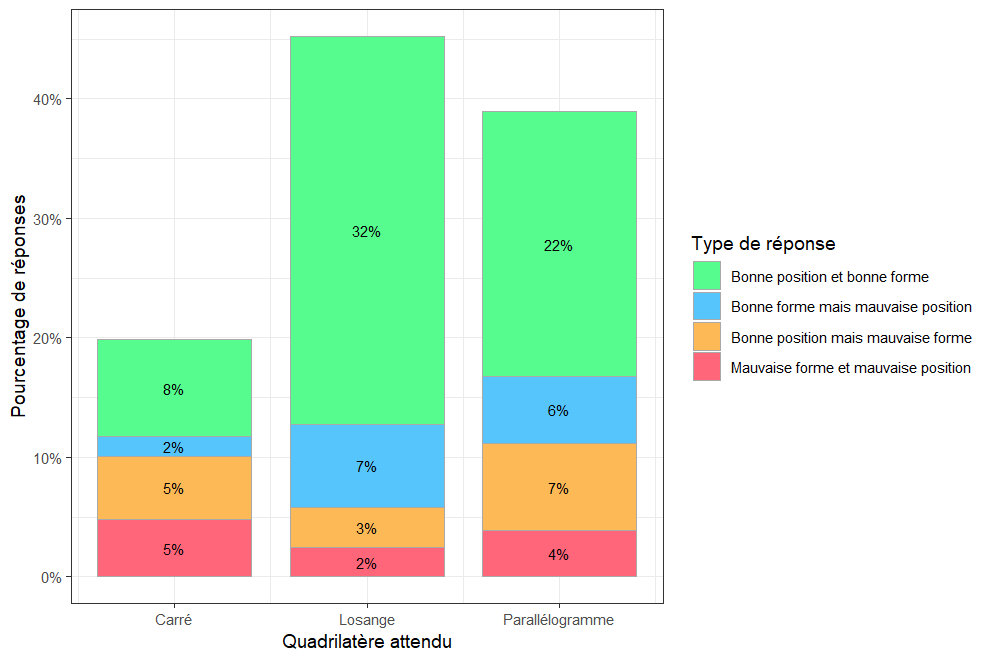
Figure 28. Histogramme de la répartition du type de quadrilatère perçu en fonction de sa position dans l’image
Nous pouvons observer que les réponses correctes, c’est-à-dire la perception de la bonne forme à la bonne position dans l’image, pour le losange et le parallélogramme sont dominantes (avec une plus grande dominance pour le losange). Les participants ont donc plus tendance à voir des losanges dans les images que les autres quadrilatères.
Les éléments d’induction pour les losanges semblent être meilleurs que les autres quadrilatères cités dans l’expérience. Une explication pourrait être que la construction des quadrilatères en forme de losange paraît plus familière dans les environnements choisis (ici des forêts et des montagnes).
Un point intéressant peut être l’angle des “pac-man” qui peuvent influencer sur la facilité à percevoir les formes ou non.
2.3 ) Analyse des données

Figure 29. Nuage de points montrant les notes moyennes de réalisme des images en fonction de leur note IMDB. Les lignes vertes représentent les moyennes des notes de confiance (horizontale) et de réalisme (verticale)
Sur la figure 29, nous pouvons observer que la majorité des images se regroupent dans la zone correspondant à une forte perception de forme (confiance élevée) mais à un réalisme faible. Cela suggère que, dans nos images, les participants reconnaissent plus facilement les figures lorsque l’environnement de l’image est stylisé ou moins réaliste. Cela pourrait s’expliquer par le fait que les éléments déclencheurs de l’illusion (comme les “pac-man”) sont plus visibles ou moins noyés dans le décor lorsque l’image est moins détaillée.
A l’inverse, très peu d’images figurent dans la zone confiance élevée et le réalisme élevé. Ce qui est en accord avec notre mini-expérience réalisée pour optimiser les hyperparamètres : en effet, nous avions remarqué qu’il y avait une corrélation négative entre le réalisme de l’image et la visibilité de l’illusion.
Ce nuage de points a aussi la particularité de nous donner les identifiants de quelques images particulières que nous étudierons dans la prochaine partie.
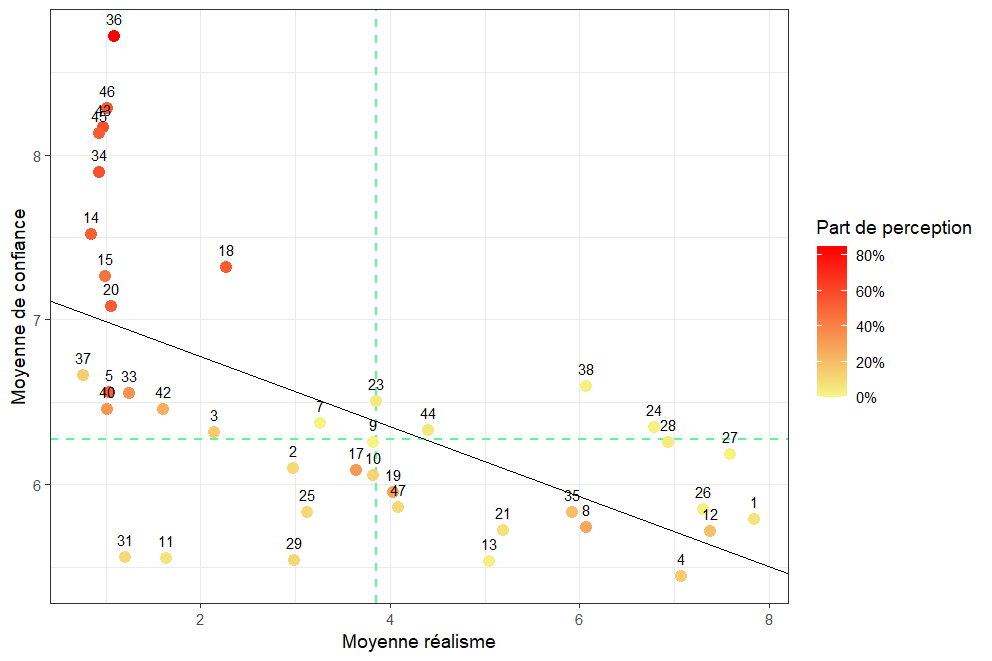
Figure 30. Régression linéaire des données du nuage de points
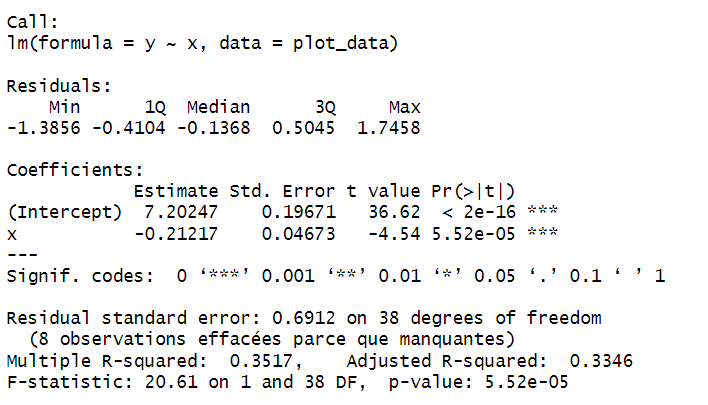
Figure 31. Résultat de la fonction summary dans Rstudio de la régression linéaire
Pour appuyer nos observations visuelles, nous avons réalisé une régression linéaire entre la moyenne de réalisme et la moyenne de confiance (calculée avec la formule IMDb). La pente obtenue est négative (≈ -0,21), ce qui signifie que plus une image est jugée réaliste, moins les participants semblent confiants dans leur perception de l’illusion. Ce résultat va dans le même sens que ce que nous avions remarqué lors de notre expérience sur les hyperparamètres : une image très réaliste rend l’illusion plus difficile à percevoir.
Ce résultat est statistiquement significatif (p < 0.00001), ce qui montre que cette relation décroissante n’est pas due au hasard. Le R² ajusté du modèle est de 0.352, ce qui veut dire que près de 35 % des variations dans la confiance des participants peuvent s’expliquer par le niveau de réalisme perçu. Même si ce n’est pas énorme, cela reste une part non négligeable dans une tâche subjective comme celle-ci, où beaucoup d’autres paramètres peuvent entrer en jeu.
Enfin, on remarque que les résidus sont globalement bien répartis autour de zéro, ce qui indique que le modèle tient la route. Cependant, en regardant attentivement le nuage de points, on peut voir que la tendance décroissante est en grande partie portée par un petit groupe de points situés en haut à gauche (faible réalisme, forte confiance). Ces quelques images influencent fortement la régression, et sans elles, la tendance serait sans doute moins marquée. Cela constitue une limite importante à garder en tête, et justifie le besoin d’analyses complémentaires ou de modèles plus robustes pour confirmer cette relation.
2.4 ) Analyse d'images spécifiques
Les images présentées dans cette partie sont visibles dans la partie 1. Images utilisées pour l'expérience en annexe.
L’image ID_36 est, comme nous pouvons l’observer sur la Figure 29, celle avec la meilleure moyenne IMDb de confiance. En la voyant, nous comprenons tout de suite pourquoi : cette image possède un fond uniforme d’arbres dans lequel se dégagent les “pac-man” de l’illusion de Kanizsa de manière très visible. Les “bouches” des “pac-man” sont très bien délimitées ce qui rend le losange extrêmement visible. Elle obtient une part de perception correcte égale à 85.16%, ce qui signifie que, parmi l’ensemble des participants, plus de 4 personnes sur 5 ont repéré la bonne forme (losange) au bon endroit (en bas à droite).
L’image ID_18 se distingue, quant à elle, par une combinaison inhabituelle : une confiance élevée (7,32 / 10) malgré un réalisme perçu relativement faible (2,31 / 10). Elle représente un paysage de montagnes baigné de lumière, avec une composition très travaillée : brumes, double source lumineuse, contrastes marqués… L’ensemble donne un rendu visuellement impressionnant, mais conserve un aspect artificiel, voire stylisé, expliquant sa faible note de réalisme.
L’illusion de Kanizsa y est matérialisée par un losange, situé en haut à droite de l’image. Les quatre “pac-man” sont intégrés dans un environnement dense, mais restent suffisamment visibles pour permettre à plus de la moitié des participants (53,12 %) de repérer la bonne forme, au bon endroit. Bien que le fond soit riche et complexe, les ouvertures claires des inducteurs ressortent bien sur les zones sombres des reliefs, ce qui facilite leur repérage.
Avec un poids de contrôle net de 1,05, l’illusion est présente de manière marquée, sans être trop forcée. Ce dosage intermédiaire pourrait expliquer pourquoi l’image parvient à maintenir un bon équilibre : l’illusion émerge clairement, tout en conservant une certaine subtilité. Malgré cela, des éléments comme la densité du décor ou l’éclat de la lumière dans la zone du losange peuvent distraire l’observateur et expliquer pourquoi la confiance n’atteint pas les sommets observés pour des images plus sobres comme ID_36.
ID_18 illustre donc bien comment une illusion peut rester efficace dans un environnement visuellement chargé, tant que les éléments clefs restent contrastés et bien positionnés. Cela en fait une image particulièrement intéressante pour étudier l’impact de la complexité visuelle sur la perception.
L’image ID_27 apporte un contraste (Figure 29) par une combinaison inverse à celle d’ID_18 : un réalisme perçu très élevé (7,56 / 10) associé à une confiance relativement faible (6,18 / 10). Cette image propose un paysage de montagnes baigné d’une lumière naturelle spectaculaire : forêts denses, jeux d’ombres portées, lens-flare discret et ciel limpide. L’ensemble donne un rendu presque photographique, expliquant sa note de réalisme élevée.
L’illusion de Kanizsa y prend la forme d’un parallélogramme, situé en haut à gauche de l’image. Les quatre inducteurs (“pac-man”) sont noyés dans la complexité du décor : la densité du feuillage, la multiplication des textures et les variations subtiles d’éclairage réduisent drastiquement leur visibilité. Résultat : seulement 0,78 % des participants ont repéré la bonne forme au bon endroit, ce qui traduit une perception quasi nulle de l’illusion malgré un réalisme fort.
L’illusion parvenait encore à être repérée avec un poids de contrôle net de 1,05, mais elle était nettement moins marquante à cause du réalisme de la scène. Cela montre que plus une image est détaillée et proche du réel, plus il devient difficile de percevoir les contours implicites nécessaires à l’illusion de Kanizsa. Les textures réalistes et les effets de lumière, bien qu’esthétiques, ajoutent du bruit visuel qui brouille les repères, notamment les “bouches” des pac-man, et rend la forme illusoire beaucoup moins évidente.
En somme, ID_27 illustre parfaitement comment l’excès de réalisme peut empêcher la formation de l’illusion, même lorsque les inducteurs sont correctement placés et dotés d’un poids d’injection élevé.
IV ) DISCUSSION
132 personnes ont participé à notre expérience mais nous en avons exclu 4 car l’écart type des notes attribuées était de 0, rendant cette notation vide de sens. Les personnes n’ont en fait pas pris la peine de bouger le slider, ce qui laisse donc une réponse automatique de 5/10 pour toutes les images (voir Figure 25). Nous avons décidé de retirer les données à analyser de ces 4 personnes car nous ne les avons pas jugées pertinentes. Il restait donc les données de 128 participants à analyser.
Les résultats suggèrent que, bien que les modèles de diffusion puissent générer des images visuellement réalistes intégrant des motifs proches des illusions de Kanizsa, leur capacité à produire des illusions perçues comme telles par des observateurs humains reste partielle et dépend fortement des conditions de génération. Le lien initialement pressenti entre les mécanismes cognitifs de complétion perceptive humaine et le fonctionnement des modèles génératifs s’avère plus complexe qu’anticipé.
L’analyse statistique révèle une corrélation négative entre le réalisme perçu des images et la confiance des participants dans la perception d’une illusion. Cela suggère que plus une image est jugée réaliste, plus les éléments inductifs de l’illusion (comme les "pac-man") se fondent dans l’environnement, rendant la forme moins saillante pour l’observateur. Ce constat rejoint nos observations préalables lors de l’optimisation des hyperparamètres : un équilibre délicat est à trouver entre réalisme et visibilité de l’illusion, notamment à travers le réglage du control weight.
En outre, le type de quadrilatère semble influer sur la perception : les losanges sont mieux reconnus que les carrés ou parallélogrammes, ce qui pourrait s'expliquer par leur familiarité dans les environnements naturels utilisés. Ce résultat soulève des questions sur le rôle des régularités contextuelles et des attentes perceptives dans l’apparition des illusions.
Un autre point important à soulever est que les éléments inductifs à eux seuls permettent aux participants de savoir si un quadrilatère est présent, sans même voir réellement la délimitation du quadrilatère. Par exemple : pour l’image 10, on peut percevoir les pac-man mais le carré n’est pas présent sur l’image. Pourtant presque 12% des participants disent voir le carré au bon endroit et ont juste. On peut interpréter ceci par un esprit de compétitivité des participants qui veulent avoir un maximum de bonnes réponses en créant des stratégies de compensation.
Ces résultats ouvrent ainsi sur une double réflexion : d’une part, sur les conditions techniques permettant à une IA de simuler des illusions perceptives crédibles, et d’autre part, sur les différences fondamentales entre les généralisations statistiques apprises par un réseau de neurones et les mécanismes neurocognitifs humains. La poursuite de ce travail pourrait explorer l’intégration explicite de contraintes perceptives dans l’apprentissage des modèles, ou l’étude comparative avec d’autres illusions intégrables dans des contextes écologiques variés.
La méthodologie employée, bien qu’efficace, présente certaines limites : le biais induit par les sliders initialement positionnés à 5 a probablement influé sur la distribution des notes, et le faible nombre d’images contrôle limite la robustesse des comparaisons. Une idée pour remédier à ce problème peut être de remplacer le slider par une échelle.
Les participants démarrent avec une note incorrecte (qui sort de l’intervalle 0-10) et avec des boutons peuvent augmenter ou diminuer les valeurs. Cela les obligerait à répondre à ces questions.
Il aurait également été intéressant de mettre une note de certitude même lorsque les participants ne voient pas de quadrilatère (question 2). Cela nous aurait permis de comparer les notes de certitudes entre les quadrilatères et les images contrôle.
Malgré cela, les réponses recueillies offrent un premier aperçu encourageant de la manière dont une IA peut suggérer, mais non "percevoir", des illusions visuelles.
Il faut également noter que l’optimisation des hyperparamètres n’est pas à son plein potentiel. Nous avons optimisé les hyperparamètres pour un carré plus grand et présent uniquement au centre de l’image (voir les images de notre expérience). Donc quand nous avions décidé entre-temps de diversifier les quadrilatères et les positions d’apparition, les hyperparamètres ont perdu de leur optimisation. Le but était de réduire la différence entre réalisme et perception d’une illusion grâce aux hyperparamètres, mais dans l’expérience, nous retrouvons des images très réalistes sans illusion et des images peu réalistes avec une illusion.
Après l’analyse des données, nous nous sommes rendu compte qu’il aurait été intéressant de poser une question supplémentaire pour connaître la certitude des participants à avoir répondu “non” à la question sur la perception d’un quadrilatère (la question 2). Cela nous aurait aidé pour les images contrôle de savoir si les participants étaient bien sûrs de n’avoir pas vu de quadrilatères.
Un autre point intéressant aurait été de demander aux participants s’ils avaient trouvé l’expérience difficile ou non, et également de leur demander s’ils avaient mis en place des stratégies pour repérer les quadrilatères.
Les images de contrôle sont au nombre de 3, il y en a une pour chaque weight, au même titre que chaque autre image. Le fait est que ce sont les formes qui nous intéressent, et non les images en elles-mêmes. Etant donné que pour chaque forme il existe 5 variations de position, donc 5 images par forme, nous aurions dû avoir 5 images contrôle pour avoir autant d’images contrôle finales que de formes, c'est-à-dire 15. La différence entre le nombre d’images contrôle et le nombre d’images par forme les rend donc malheureusement difficilement exploitables.
Une autre possibilité d’amélioration, cette fois plus générale au monde de la recherche, serait de rendre accessible les codes qui permettent d’obtenir les résultats des études scientifiques.
En effet, dans de nombreux articles, bien que les résultats soient décrits, le code qui a permis de les obtenir n’est pas partagé et cela nuit à la reproductibilité des expériences. Si ce partage est possible, il permettrait à d’autres chercheurs de valider les résultats, de les répliquer, mais aussi de les adapter ou de les améliorer. Par exemple, durant notre projet, certains articles sur la génération d’illusions d’optique à l’aide de modèles de diffusion ne mettaient pas à disposition leur code : il nous a donc fallu reconstruire les étapes par nous-mêmes, ce qui demande du temps. L’usage de plateformes de partage de code telles que GitHub accélérerait les découvertes et encouragerait des collaborations plus transparentes entre chercheurs.
V ) CONCLUSION
Cette étude s'est concentrée sur l'exploration de la capacité des modèles de diffusion à générer des images contenant des illusions visuelles de type Kanizsa dans des contextes réalistes. En combinant des principes issus de la psychologie cognitive, de la modélisation par intelligence artificielle et de l'évaluation perceptive humaine, un protocole expérimental a été mis en œuvre, associant la génération d'images algorithmiques et la validation par des participants humains.
Les résultats obtenus confirment la possibilité de générer des images où les observateurs perçoivent des formes illusoires de Kanizsa sans qu'elles soient explicitement tracées. Cependant, il est apparu clairement que cette perception est étroitement liée à plusieurs facteurs, incluant le degré de réalisme de l'image générée, la forme spécifique du quadrilatère illusoire, sa position spatiale, ainsi que des paramètres techniques du modèle tels que le control weight. Nous avons notamment observé un compromis notable entre le réalisme de l'image et la visibilité de l'illusion, suggérant qu'un réalisme excessif tend à rendre les éléments inductifs moins saillants, diluant l'illusion dans la complexité du décor. De plus, la forme de l'illusion a montré une influence sur la perception, les losanges étant mieux reconnus dans les environnements utilisés que les carrés ou parallélogrammes. Il a également été souligné que les éléments inductifs seuls pouvaient orienter la réponse des participants quant à la présence d'un quadrilatère, même si l'illusion complète n'était pas perçue.
Au-delà de la performance technique de la génération d'images, cette recherche soulève des questions fondamentales concernant la comparaison entre les processus appris par les modèles de diffusion et les mécanismes perceptifs humains. Alors que le cerveau humain s'appuie sur des lois perceptives complexes et des mécanismes de rétroaction corticale pour compléter les informations manquantes et construire une perception unifiée du monde, les IA génératives fonctionnent en identifiant des régularités statistiques dans d'énormes ensembles de données, sans une compréhension intrinsèque du monde physique ou des principes perceptifs sous-jacents.
Ce travail préliminaire, bien qu'informatif, a également mis en évidence certaines limites méthodologiques qui pourraient être améliorées dans de futures études. Parmi elles, le biais potentiel introduit par la valeur initiale des sliders pour les évaluations de réalisme et de certitude, ainsi que le nombre limité d'images contrôle, qui a rendu certaines comparaisons difficiles. L'optimisation des hyperparamètres, initialement ciblée sur une forme et une position uniques, a également perdu de son efficacité lors de la diversification des stimuli dans l'expérience principale.
Ces observations ouvrent la voie à de multiples perspectives de recherche. Il serait pertinent d'explorer l'application de modèles de diffusion à d'autres types d'illusions visuelles ou dans des environnements plus variés afin d'évaluer la possibilité de généraliser ces résultats. L'affinage des techniques de génération pour mieux intégrer des contraintes inspirées des théories de la perception humaine, comme la Gestalt ou les principes de rétroaction, pourrait potentiellement améliorer la capacité de l'IA à suggérer des illusions crédibles. Une piste particulièrement intéressante serait de tenter de modifier l'entraînement ou la structure des modèles de diffusion pour qu'ils parviennent à "percevoir" ou à reproduire les illusions de Kanizsa d'une manière plus analogue aux processus cognitifs humains, en s'inspirant notamment des boucles de rétroactions présentes dans le cortex visuel. Enfin, le partage ouvert des codes et des données expérimentales, tel qu'utilisé pour nos analyses, contribuerait significativement à la transparence et à l'avancement collaboratif dans ce domaine de recherche émergent.
En conclusion, cette étude interdisciplinaire, à l'intersection de l'intelligence artificielle, de la vision humaine et de la génération d'images, a permis de documenter la capacité des modèles de diffusion à suggérer des illusions perceptives. Elle souligne à la fois le potentiel de ces outils génératifs et les différences fondamentales qui persistent entre la création d'images par une machine et la complexité de la perception humaine.
VI ) BIBLIOGRAPHIE
[1] Boden, M. A. (2014). GOFAI. In K. Frankish & W. M. Ramsey (Eds.), The Cambridge handbook of artificial intelligence (Chap. 4). Cambridge University Press;
[2] Geng, D., Park, I., & Owens, A. (2025, janvier 10). Factorized diffusion: Perceptual illusions by noise decomposition (arXiv:2404.11615v2). arXiv;
https://arxiv.org/abs/2404.11615
[3] Kartable. (s. d.). Aires cérébrales et plasticité;
https://www.kartable.fr/ressources/svt/cours/aires-cerebrales-et-plasticite/19144
[4] Frédérique Faïta, Université de Bordeaux. (s. d.). La perception – Cours de vision;
[5] Delacour, J. (2001). Conscience et cerveau (Chap. 3, « Neurobiologie des représentations conscientes »). Paris : Odile Jacob.
[6] Gaio Mauro, Madelaine Jacques. Un modèle de l'illusion perceptive : simulation versus expérimentation. In: Intellectica. Revue de l'Association pour la Recherche Cognitive, n°22, 1996/1. L’expérimentation et l’intelligence artificielle. pp. 67-91;
https://doi.org/10.3406/intel.1996.1516
[7] Lvmin Zhang, (2023). Let us control diffusion models! ;